Algoritmo III – Um passo além ... continuação
Esse artigo é continuação de
Algoritmo III – Um passo além da teoria. Onde ficou faltando exemplificarmos a estrutura de desvio condicional aninhado. Pretendo agora completar o que ficou pendente e, na mesma linha de abordagem que venho adotando ao falar sobre algoritmos, aproveitar também para destacar alguns pontos importantes que implicam na aplicação pratica do conhecimento sobre algoritmos. Portanto, além de mostrar exemplos da implementação do algoritmo em diferentes linguagens, criarei versões diferentes do mesmo exemplo onde demonstrarei o efeito da modularização, suas vantagens, bem como apontar uma caminho de como fazer isso. Que lógica seguir, qual o alvo buscar na hora de pensar em modularizar um programa.
Agora que está claro o que iremos fazer, falta explicar o “como”. Usarei um único algoritmo. Um que seja muito simples. Ao ponto de a única coisa nele que vale apena ser mencionada é o fato que ele implementa a estrutura de desvio condicional aninhado. Desta forma estamos focados no que tange ao conceito lógico que desejamos abordar. Por isso o algoritmo escolhido será o tradicional e simplório algoritmo de verificação do maior e o menor valor entre três números. Delphi e Java, a princípio, são as linguagens que usarei. Quanto a modularização, iniciaremos com o um primeiro exemplo bem primário onde codificarei o programa de forma seqüencial, todo num único fluxo. Forma mais comumente adotada (infelizmente). Em seguida, numa segunda versão evoluiremos o primerio exemplo aplicando um nível de modularização sob uma perspectiva estruturada. Para finalizar, construiremos uma terceira versão aumentando o grau de modularização sob uma perspectiva OO. O fato de neste terceiro exemplo o grau de modularização ser maior que o anterior não está diretamente relacionado com a abordagem OO. Ou seja, também é possível alcançar o mesmo grau usando estruturação.
Partiremos agora para a construção do primeiro exemplo do algoritmo que determina o Maior e o Menor valor entre três valores digitados.
Algoritmo não modularizado – aplicando a estrutura de decisão “desvio condicional”: Esse é o nosso ponto de partida ...
PROGRAMA DeterminaMaiorMenor;
VARIÁVEIS
Num1Zn, Num2Zn, Num3Zn: NUMÉRICO;
INÍCIO
LEIA (Num1Zn, Num2Zn, Num3Zn);
// Determinando o maior valor
SE (Num1Zn > Num2Zn) E (Num1Zn > Num3Zn) ENTÃO
ESCREVER (“Maior = ” + Num1Zn)
SENÃO SE (Num2Zn > Num1Zn) E (Num2Zn > Num3Zn) ENTÃO
ESCREVER (“Maior = ” + Num2Zn)
SENÃO
ESCREVER (“Maior = ” + Num3Zn);
// Determinando o menor valor
SE (Num1Zn < Num2Zn) E (Num1Zn < Num3Zn) ENTÃO
ESCREVER (“Menor = ” + Num1Zn)
SENÃO SE (Num2Zn < Num1Zn) E (Num2Zn < Num3Zn) ENTÃO
ESCREVER (“Menor = ” + Num2Zn)
SENÃO
ESCREVER (“Menor = ” + Num3Zn)
FIM.
O algoritmo não deve apresentar detalhes específicos da tecnologia definida pela linguagem. Por isso você vai perceber que na implementação do algoritmo numa linguagem vai aparecer linhas de código a mais, que objetivam lidar com detalhes exclusivos da tecnologia. Entretanto, o algoritmo pode e deve apresentar uma modularização adequada. Veremos adiante.
Implementando o algoritmo não modularizado em Delphi
procedure TForm1.Button1Click(Sender: TObject);
var
Num1Zn, Num2Zn, Num3Zn, ZnMaior, ZnMenor: Double;
StrNum1Zn, StrNum2Zn, StrNum3Zn, MsgSaida: String;
SaoIguais: boolean ;
begin
// Entrada de dados
StrNum1Zn := InputBox('www.estacaozn.blogspot.com | Encontra o Maior Valor', 'Digite o número', '');
StrNum2Zn := InputBox('www.estacaozn.blogspot.com | Encontra o Maior Valor', 'Digite o número', '');
StrNum3Zn := InputBox('www.estacaozn.blogspot.com | Encontra o Maior Valor', 'Digite o número', '');
// Processamento
Num1Zn := StrToFloat(StrNum1Zn);// convertendo de string para Double
Num2Zn := StrToFloat(StrNum2Zn);// convertendo de string para Double
Num3Zn := StrToFloat(StrNum3Zn);// convertendo de string para Double
// Comparando para encontrar o maior
(***********************************)
(* Antes, testo se eles são iguais *)
SaoIguais := (Num1Zn = Num2Zn) and (Num1Zn = Num3Zn);
if SaoIguais then
begin
msgSaida := 'Os números são iguais - %f';
ZnMaior := Num1Zn;
end
else
begin
// Determinando o maior valor
msgSaida := 'O maior número é: %f';
if ((Num1Zn > Num2Zn) and (Num1Zn > Num3Zn)) then
ZnMaior := Num1Zn
else if ((Num2Zn > Num1Zn) and (Num2Zn > Num3Zn)) then
ZnMaior := Num2Zn
else
ZnMaior := Num3Zn;
// Determinando o menor valor
msgSaida := msgSaida + ' | O menoor número é: %f';
if ((Num1Zn < Num2Zn) and (Num1Zn < Num3Zn)) then
ZnMenor := Num1Zn
else if ((Num2Zn < Num1Zn) and (Num2Zn < Num3Zn)) then
ZnMenor := Num2Zn
else
ZnMenor := Num3Zn;
end;
(*Saída de dados*)
Self.Canvas.Refresh;
Self.Canvas.TextOut(12, 70, 'www.estacaozn.blogspot.com');
Self.Canvas.TextOut(12, 100, Format(MsgSaida, [ZnMaior, ZnMenor]));
end;
Observe que temos código demais para uma tarefa tão simples ...
Implementando o algoritmo não modularizado em Java
package verificamaiorzn;
import javax.swing.JOptionPane;
/**
*
* @author GMottaZn
*/
public class Main {
/**
* @param args the command line arguments
*/
public static void main(String[] args) {
String strNum1Zn, strNum2Zn, strNum3Zn,msgSaida;
double Num1Zn, Num2Zn, Num3Zn, ZnMaior, ZnMenor;
boolean saoIguais;
// Entrada de dados
strNum1Zn = JOptionPane.showInputDialog("Digite o primeiro zn número");
strNum2Zn = JOptionPane.showInputDialog("Digite o segundo zn número");
strNum3Zn = JOptionPane.showInputDialog("Digite o terceiro zn número");
// processamento
Num1Zn = Double.parseDouble(strNum1Zn); // convertendo de string para Double
Num2Zn = Double.parseDouble(strNum2Zn); // convertendo de string para Double
Num3Zn = Double.parseDouble(strNum3Zn); // convertendo de string para Double
// Comparando para encontrar o maior
// Antes, testo se eles são iguais
saoIguais = (Num1Zn == Num2Zn) && (Num1Zn == Num3Zn);
if (saoIguais){
msgSaida = "Os números são iguais - ";
ZnMaior = Num1Zn;
}// então procuro o maior
else {
msgSaida = "O maior número é: ";
if ((Num1Zn > Num2Zn) &&(Num1Zn > Num3Zn)){
ZnMaior = Num1Zn;
}
else {
if ((Num2Zn > Num1Zn) &&(Num2Zn > Num3Zn)){
ZnMaior = Num2Zn;
}
else
ZnMaior = Num3Zn;
};
//Determina o menor valor
msgSaida = msgSaida + " | O menor número é: ";
if ((Num1Zn < Num2Zn) &&(Num1Zn < Num3Zn)){
ZnMenor = Num1Zn;
}
else {
if ((Num2Zn < Num1Zn) &&(Num2Zn < Num3Zn)){
ZnMenor = Num2Zn;
}
else
ZnMenor = Num3Zn;
};
};
// Saída de dados
JOptionPane.showMessageDialog(null, " Estação Zn - " + msgSaida + ZnMaior,
"www.estacaozn.blogspot.com", JOptionPane.INFORMATION_MESSAGE);
// Finaliza programa
System.exit(0);
}
}
Modificando o Algoritmo para que ele apresente o primeiro nível de modularização. Vamos transformar o fluxo que determina o maior valor e transformar numa
sub-rotina (um sub-programa). Faremos o mesmo para o segundo fluxo, o que determina o menor valor. Logo, teremos nosso algoritmo modularizado em duas sub-rotinas independentes, cada uma com um objetivo específico.
PROGRAMA DeterminaMaiorMenor;
VARIÁVEIS
Num1Zn, Num2Zn, Num3Zn: NUMÉRICO;
// primeira sub-rotina
Função EncontraMaior(Num1Zn, Num2Zn, Num3Zn: Double): String;
Constatnte
MsgSaida = 'O maior número é: ;
var
ZnMaior: Double;
Início
// Determinando o maior valor
SE (Num1Zn > Num2Zn) E (Num1Zn > Num3Zn) ENTÃO
ZnMaior := Num1Zn
SENÃO SE (Num2Zn > Num1Zn) E (Num2Zn > Num3Zn) ENTÃO
ZnMaior := Num2Zn)
SENÃO
ZnMaior := Num3Zn);
EncontraMaior := MsgSaida + ZnMaior;
Fim;
// segunda sub-rotina
Função EncontraMenor(Num1Zn, Num2Zn, Num3Zn: Double): String;
Constatnte
MsgSaida = 'O maior número é: ;
var
ZnMenor: Double;
Início
// Determinando o menor valor
SE (Num1Zn < Num2Zn) E (Num1Zn < Num3Zn) ENTÃO
ZnMenor := Num1Zn
SENÃO SE (Num2Zn < Num1Zn) E (Num2Zn < Num3Zn) ENTÃO
ZnMenor := Num2Zn)
SENÃO
ZnMenor := Num3Zn);
EncontraMenor := MsgSaida + ZnMenor;
Fim;
função SaoIguais(Num1Zn, Num2Zn, Num3Zn: Double): Boolean;
Início
SaoIguais := (Num1Zn = Num2Zn) and (Num1Zn = Num3Zn);
Fim;
//Programa principal
INÍCIO
LEIA (Num1Zn, Num2Zn, Num3Zn);
SE SaoIguais(Num1Zn, Num2Zn, Num3Zn) ENTÃO
ESCREVA(“Os números são iguais”)
SENÃO
INÍCIO
ESCREVA(“O menor número é: ” + EncontraMenor(Num1Zn, Num2Zn, Num3Zn));
ESCREVA(“O maior número é: ” + EncontraMaior(Num1Zn, Num2Zn, Num3Zn));
FIM;
FIM.
Sub-Rotina – Comumente chamamos as sub-rotinas de “Procedimentos” (procedure) ou “Funções” (function). Podemos entendê-las como um trecho de programa escrito separadamente.
Implementando o algoritmo modularizado em Delphi
function EncontraMaior(const Num1Zn, Num2Zn, Num3Zn: Double): String;
const
MsgSaida = 'O maior número é: %f';
var
ZnMaior: Double;
begin
// Determinando o maior valor
if ((Num1Zn > Num2Zn) and (Num1Zn > Num3Zn)) then
ZnMaior := Num1Zn
else if ((Num2Zn > Num1Zn) and (Num2Zn > Num3Zn)) then
ZnMaior := Num2Zn
else
ZnMaior := Num3Zn;
Result := Format(MsgSaida, [ZnMaior]);
end;
function EncontraMenor(const Num1Zn, Num2Zn, Num3Zn: Double): String;
const
MsgSaida = 'O menor número é: %f';
var
ZnMaior: Double;
begin
// Determinando o menor valor
if ((Num1Zn < Num2Zn) and (Num1Zn < Num3Zn)) then
ZnMaior := Num1Zn
else if ((Num2Zn < Num1Zn) and (Num2Zn < Num3Zn)) then
ZnMaior := Num2Zn
else
ZnMaior := Num3Zn;
Result := Format(MsgSaida, [ZnMaior]);
end;
Verificar se os valores são iguais é um plus ... então vai ...
function SaoIguais(const Num1Zn, Num2Zn, Num3Zn: Double; var MsgSaida: String): Boolean;
const
AMsgSaida = 'Os números são iguais: %f';
begin
Result := (Num1Zn = Num2Zn) and (Num1Zn = Num3Zn);
if Result then
MsgSaida := Format(AMsgSaida, [Num1Zn]);
end;
A seguir codificaremos o programa principal "DeterminaMaiorMenor"
procedure TForm1.Button2Click(Sender: TObject);
var
Num1Zn, Num2Zn, Num3Zn: Double;
StrNum1Zn, StrNum2Zn, StrNum3Zn, MsgSaida: String;
begin
// Entrada de dados
StrNum1Zn := InputBox('www.estacaozn.blogspot.com | Encontra o Maior Valor',
'Digite o número', '');
StrNum2Zn := InputBox('www.estacaozn.blogspot.com | Encontra o Maior Valor',
'Digite o número', '');
StrNum3Zn := InputBox('www.estacaozn.blogspot.com | Encontra o Maior Valor',
'Digite o número', '');
// Processamento
Num1Zn := StrToFloat(StrNum1Zn);// convertendo de string para Double
Num2Zn := StrToFloat(StrNum2Zn);// convertendo de string para Double
Num3Zn := StrToFloat(StrNum3Zn);// convertendo de string para Double
if not (SaoIguais(Num1Zn, Num2Zn, Num3Zn, MsgSaida)) then
begin
MsgSaida := EncontraMaior(Num1Zn, Num2Zn, Num3Zn);
MsgSaida := MsgSaida + ' | ' + EncontraMenor(Num1Zn, Num2Zn, Num3Zn);
end;
(*Saída de dados*)
Self.Canvas.Refresh;
Self.Canvas.TextOut(12, 70, 'www.estacaozn.blogspot.com');
Self.Canvas.TextOut(12, 100, MsgSaida);
end;
Observe que o número de linhas do programa principal diminuiu sensivelmente. Entretanto, o que é pouco comentado a respeito de modularização é que a quantidade de variáveis também tende a reduzir. Isso é um ganho muito importante na qualidade do seu código. Note que reduzimos de dez variáveis no primeiro exemplo para sete no segundo.
Implementando o algoritmo modularizado em Java
package verificamaiormenor;
import javax.swing.JOptionPane; // Importando pacote de extenção Java API
/**
*
* @author GMottaZn
*/
public class Main {
// Atributos privados
private double num3Zn;
private double num2Zn;
private double num1Zn;
private String znMsgSaida;
public double getNum3Zn() {
return num3Zn;
}
public void setNum3Zn(double num3Zn) {
this.num3Zn = num3Zn;
}
public double getNum2Zn() {
return num2Zn;
}
public void setNum2Zn(double num2Zn) {
this.num2Zn = num2Zn;
}
public double getNum1Zn() {
return num1Zn;
}
public void setNum1Zn(double num1Zn) {
this.num1Zn = num1Zn;
}
public String getZnMsgSaida() {
return znMsgSaida;
}
public void setZnMsgSaida(String znMsgSaida) {
this.znMsgSaida = znMsgSaida;
}
// Metodos privados
private String encontraMaior() {
double znMaior;
if ((getNum1Zn() > getNum2Zn()) && (getNum1Zn() > getNum3Zn())) {
znMaior = getNum1Zn();
}
else {
if ((getNum2Zn() > getNum1Zn()) && (getNum2Zn() > getNum3Zn())) {
znMaior = getNum2Zn();
}
else {
znMaior = getNum3Zn();
}
}
return "O Maior Número é: " + znMaior;
}
private String encontraMenor() {
double znMenor;
if ((getNum1Zn() < getNum2Zn()) && (getNum1Zn() < getNum3Zn())) {
znMenor = getNum1Zn();
}
else {
if ((getNum2Zn() < getNum1Zn()) && (getNum2Zn()< getNum3Zn())) {
znMenor = getNum2Zn();
}
else {
znMenor = getNum3Zn();
}
}
return "O Menor Número é: " + znMenor;
}
private boolean saoIguais(){
return (getNum1Zn() == getNum2Zn()) && (getNum1Zn() == getNum3Zn());
}
// Método Público
public void executaVerificacao(){
String saidaMaior, saidaMenor;
if (saoIguais()){
saidaMaior = "Os números são iguais: " + getNum1Zn();
setZnMsgSaida(saidaMaior);
}
else{
saidaMaior = encontraMaior();
saidaMenor = encontraMenor();
setZnMsgSaida(saidaMaior + " | " + saidaMenor);
}
}
public static void main(String[] args) {
String strNum1Zn, strNum2Zn, strNum3Zn, msgSaida;
// Entrada de dados ...
strNum1Zn = JOptionPane.showInputDialog("Digite o primeiro zn número");
strNum2Zn = JOptionPane.showInputDialog("Digite o segundo zn número");
strNum3Zn = JOptionPane.showInputDialog("Digite o terceiro zn número");
/**
* Instanciando um objeto cujo o tipo é a classe "Main".
* O construtor "Main()" retorna um referencia de memória para a variável "MyZnClass"
*/
Main MyZnClass = new Main();
// Atribuindo valor aos atributos
MyZnClass.setNum1Zn(Double.parseDouble(strNum1Zn));
MyZnClass.setNum2Zn(Double.parseDouble(strNum2Zn));
MyZnClass.setNum3Zn(Double.parseDouble(strNum3Zn));
//PROCESSA a verificação para encontrar o maior e o menor valor
MyZnClass.executaVerificacao();
// Saída de dados
JOptionPane.showMessageDialog(null, " Estação Zn - " +
MyZnClass.getZnMsgSaida(), "www.estacaozn.blogspot.com",
JOptionPane.INFORMATION_MESSAGE);
// Finaliza programa
System.exit(0);
}
}
Este tipo modularização, em linguagens como o Java apresnta pouca melhoria em termos visuais como, por exemplo, comparado ao Delphi. Isso se olharmos o todo do programa. Entretanto, se considerarmos apenas o programa principal, que se inicia na linha 101 (public static void main(String[] args)) é nítido o ganho na qualidade do código.
Chegamos a um nível de complexidade mais avançado do tema proposto. Caminhamos progressivamente no sentido de fornecer conteúdo pratico e teórico(veja sub-rotinas e O princípio da caixa preta) para fortalecer o ponto de vista que estou tentando apresentar. Vamos aumentar o grau de modularização do nosso simplório algoritmo usando a orientação a objetos.
Implementando o algoritmo modularizado em Delphi
primeiro codificaremos a classe que encontrará o maior e o menor valor...
unit DeterminaMaiorMenorZN;
interface
uses
classes, SysUtils;
(*********************************************************************
* Nesta unit definimos uma Classe que possui um comportamento capaz *
* de determinar qual o maior e o menor valor entre três valores *
* atribuidos a ela. (GMttaZn - 07/2008) *
********************************************************************)
type
TDeterminaMaiorMenorZN = Class(TComponent)
private
(* Atributos Privados *)
FNum3Zn: Double;
FNum1Zn: Double;
FNum2Zn: Double;
FZnMsgSaida: String;
(* métodos setters *)
procedure SetNum1Zn(const Value: Double);
procedure SetNum2Zn(const Value: Double);
procedure SetNum3Zn(const Value: Double);
procedure SetZnMsgSaida(const Value: String);
(* Metodos privados *)
function EncontraMaior: Double;
function EncontraMenor: Double;
function SaoIguais: boolean;
public
procedure ExecutaVerificacao;
(* Propriedades - são os getters e setters em Delphi *)
property Num3Zn: Double read FNum3Zn write Setnum3Zn;
property Num2Zn: Double read FNum2Zn write Setnum2Zn;
property Num1Zn: Double read FNum1Zn write Setnum1Zn;
property ZnMsgSaida: String read FZnMsgSaida write SetznMsgSaida;
end;
implementation
const
// Definindo constantes
MSG_MAIOR_ZN = 'Maior Número = %f';
MSG_MENOR_ZN = 'Menor Número = %f';
MSG_IGUAIS_ZN = 'São Iguais = %f';
{ TDeterminaMaiorMenorZN }
(**********************************************************
* Inmplementa um algoritmo para determinar o maior entre *
* três valores - http://estacaozn.blogspot.com *
**********************************************************)
function TDeterminaMaiorMenorZN.EncontraMaior: Double;
begin
if ((FNum1Zn > FNum2Zn) and (FNum1Zn > FNum3Zn)) then
Result := Num1Zn
else if ((FNum2Zn > FNum1Zn) and (FNum2Zn > FNum3Zn)) then
Result := FNum2Zn
else
Result := FNum3Zn;
end;
(**********************************************************
* Inmplementa um algoritmo para determinar o menor entre *
* três valores - http://estacaozn.blogspot.com *
**********************************************************)
function TDeterminaMaiorMenorZN.EncontraMenor: Double;
begin
if ((FNum1Zn < FNum2Zn) and (FNum1Zn < FNum3Zn)) then
Result := Num1Zn
else if ((FNum2Zn < FNum1Zn) and (FNum2Zn < FNum3Zn)) then
Result := FNum2Zn
else
Result := FNum3Zn;
end;
(*****************************************************************************
* Evoca os métodos que determinam o maior e o menor valor dos atributos *
* da classe. Testando, primeiramente se os valores não são iguais. Desta *
* forma então, definido um valor adequado para a saída. *
* - http://estacaozn.blogspot.com *
*****************************************************************************)
procedure TDeterminaMaiorMenorZN.ExecutaVerificacao;
var
SaidaMaior, SaidaMenor: String ;
begin
if (SaoIguais) then
SetZnMsgSaida(Format(MSG_IGUAIS_ZN, [Num1Zn]))
else
begin
SaidaMaior := Format(MSG_MAIOR_ZN, [EncontraMaior]);
SaidaMenor := Format(MSG_MENOR_ZN, [EncontraMenor]);
SetZnMsgSaida(SaidaMaior + ' | ' + SaidaMenor);
end;
end;
(* Determina se o valor dos atributos são guais - http://estacaozn.blogspot.com*)
function TDeterminaMaiorMenorZN.SaoIguais: boolean;
begin
Result := (Num1Zn = Num2Zn) and (Num1Zn = Num3Zn);
end;
procedure TDeterminaMaiorMenorZN.Setnum1Zn(const Value: double);
begin
FNum1Zn := Value;
end;
procedure TDeterminaMaiorMenorZN.Setnum2Zn(const Value: double);
begin
FNum2Zn := Value;
end;
procedure TDeterminaMaiorMenorZN.Setnum3Zn(const Value: double);
begin
FNum3Zn := Value;
end;
procedure TDeterminaMaiorMenorZN.SetznMsgSaida(const Value: String);
begin
FZnMsgSaida := Value;
end;
end.
Program principal - no contexto da nossa modularização
procedure TForm1.Button3Click(Sender: TObject);
var
MyDeterminaMaiorMenorZn: TDeterminaMaiorMenorZN;
StrNum1Zn, StrNum2Zn, StrNum3Zn, MsgSaida: String;
begin
// Entrada de dados
StrNum1Zn := InputBox('www.estacaozn.blogspot.com | Encontra o Maior Valor',
'Digite o número', '');
StrNum2Zn := InputBox('www.estacaozn.blogspot.com | Encontra o Maior Valor',
'Digite o número', '');
StrNum3Zn := InputBox('www.estacaozn.blogspot.com | Encontra o Maior Valor',
'Digite o número', '');
// Processamento
MyDeterminaMaiorMenorZn := TDeterminaMaiorMenorZN.Create(Self);
try
MyDeterminaMaiorMenorZn.Num1Zn := StrToFloat(StrNum1Zn);// convertendo de string para Double
MyDeterminaMaiorMenorZn.Num2Zn := StrToFloat(StrNum2Zn);// convertendo de string para Double
MyDeterminaMaiorMenorZn.Num3Zn := StrToFloat(StrNum3Zn);// convertendo de string para Double
MyDeterminaMaiorMenorZn.ExecutaVerificacao;
(*Saída de dados*)
Self.Repaint;
//Self.Canvas.Refresh;
Self.Canvas.TextOut(250, 90, 'www.estacaozn.blogspot.com');
Self.Canvas.TextOut(250, 110, MyDeterminaMaiormenorZn.ZnMsgSaida);
finally
MyDeterminaMaiorMenorZn.Free;
end;
end;
Note no exemplo acima que a quantidade de varaáveis foi reduzido ainda mais.
Implementando o algoritmo modularizado em Java
Primeiro a classe responsável por determinar o maior e o menor valor
package modularizandoverificamaiormenoroo;
/**
*
* @author GMottaZN
* www.estacaozn.blogspot.com
* Este exemplo foi construido com objetivo de demostrar
* as vantagens de mudularizar um programa. Aplicamos uma abordagem OO
* para alcançar este objetivo.
*/
public class DeterminaMaiorMenorZN {
// Atributos privados
private double num3Zn;
private double num2Zn;
private double num1Zn;
private String znMsgSaida;
// Definindo constantes
final static String MSG_MAIOR_ZN = "Maior Número = ";
final static String MSG_MENOR_ZN = "Menor Número = ";
final static String MSG_IGUAIS_ZN = "São Iguais = ";
// getters e setters
public double getNum3Zn() {
return num3Zn;
}
public void setNum3Zn(double num3Zn) {
this.num3Zn = num3Zn;
}
public double getNum2Zn() {
return num2Zn;
}
public void setNum2Zn(double num2Zn) {
this.num2Zn = num2Zn;
}
public double getNum1Zn() {
return num1Zn;
}
public void setNum1Zn(double num1Zn) {
this.num1Zn = num1Zn;
}
public String getZnMsgSaida() {
return znMsgSaida;
}
public void setZnMsgSaida(String znMsgSaida) {
this.znMsgSaida = znMsgSaida;
}
// Metodos privados
private double encontraMaior() {
/**
* Inmplementa um algoritmo para determinar o maior entre
* três valores - http://estacaozn.blogspot.com
*/
double znMaior;
if ((getNum1Zn() > getNum2Zn()) && (getNum1Zn() > getNum3Zn())) {
znMaior = getNum1Zn();
}
else {
if ((getNum2Zn() > getNum1Zn()) && (getNum2Zn() > getNum3Zn())) {
znMaior = getNum2Zn();
}
else {
znMaior = getNum3Zn();
}
}
return znMaior;
}
private double encontraMenor() {
/**
* Inmplementa um algoritmo para determinar o menor entre
* três valores - http://estacaozn.blogspot.com
*/
double znMenor;
if ((getNum1Zn() < getNum2Zn()) && (getNum1Zn() < getNum3Zn())) {
znMenor = getNum1Zn();
}
else {
if ((getNum2Zn() < getNum1Zn()) && (getNum2Zn()< getNum3Zn())) {
znMenor = getNum2Zn();
}
else {
znMenor = getNum3Zn();
}
}
return znMenor;
}
private boolean saoIguais(){
/**
* Verifica se os valores atribuidos aos atributos da classe
* são iguais - http://estacaozn.blogspot.com
*/
return (getNum1Zn() == getNum2Zn()) && (getNum1Zn() == getNum3Zn());
}
// Método Público
public void executaVerificacao(){
String saidaMaior, saidaMenor;
if (saoIguais()){
setZnMsgSaida(MSG_IGUAIS_ZN + getNum1Zn());
}
else{
saidaMaior = MSG_MAIOR_ZN + encontraMaior();
saidaMenor = MSG_MENOR_ZN + encontraMenor();
setZnMsgSaida(saidaMaior + " | " + saidaMenor);
}
}
}
Programa principal Java
package modularizandoverificamaiormenoroo;
import javax.swing.JOptionPane;
/**
*
* @author Gerson
*/
public class Main {
private static DeterminaMaiorMenorZN MyDeterminaMaiormenorZn;
/**
* @param args the command line arguments
*/
public static void main(String[] args) {
String strNum1Zn, strNum2Zn, strNum3Zn, msgSaida;
// Entrada de dados ...
strNum1Zn = JOptionPane.showInputDialog("Digite o primeiro zn número");
strNum2Zn = JOptionPane.showInputDialog("Digite o segundo zn número");
strNum3Zn = JOptionPane.showInputDialog("Digite o terceiro zn número");
/**
* Instanciando um objeto cujo o tipo é a classe "Main".
* O construtor "Main()" retorna um referencia de memória
* para a variável "MyDeterminaMaiormenorZn"
*/
MyDeterminaMaiormenorZn = new DeterminaMaiorMenorZN();
// Atribuindo valor aos atributos
MyDeterminaMaiormenorZn.setNum1Zn(Double.parseDouble(strNum1Zn));
MyDeterminaMaiormenorZn.setNum2Zn(Double.parseDouble(strNum2Zn));
MyDeterminaMaiormenorZn.setNum3Zn(Double.parseDouble(strNum3Zn));
//PROCESSA a verificação para encontrar o maior e o menor valor
MyDeterminaMaiormenorZn.executaVerificacao();
// Saída de dados
JOptionPane.showMessageDialog(null, " Estação Zn - " +
MyDeterminaMaiormenorZn.getZnMsgSaida(), "www.estacaozn.blogspot.com",
JOptionPane.INFORMATION_MESSAGE);
// Finaliza programa
System.exit(0);
}
}
Agora sim podemos dizer que temos um programa em Java. Veja que na "public class Main {", aquele aspecto de código macarrônico sumiu. Logo, estamos mais perto da luz!
A seguir, veja abaixo, através da UML, como as classes codificadas se relacionam. Usei o Jude para elaborar um diagrama de classes que modelasse o algoritmo.

Na ilustração abaixo adaptei para o contexto Delphi o diagrama de Classes
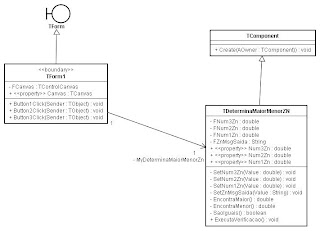
Mas qual foi a causa da terceira modularização? Será que você conseguiu perceber? Está última modularização foi a que alcançou de fato o grau máximo de funcionalidade atômica para cada sub-rotina. No exemplo anterior, as sub-rotinas “EncontraMenor” e “EncontraMaior” além de determinarem o maior e o menor, cada uma respectivamente, elas no final ainda ficaram encarregadas de fornecer o output para o usuário. Elas convertem o valor e possuem como saída a mensagem pro usuário. Isso não é legal, cada uma delas está acumulando funções diferentes e esse tipo de deslize lógico é que acaba sendo o tempero das macarronadas mais substanciosas e pesadas. Então, recodificamos cada uma das sub-rotinas para que elas possuam apenas uma funcionalidade, apenas uma responsabilidade. E transferimos para o que chamamos de programa principal a responsabilidade de comunicar ao usuário o resultado. Assim estamos mais perto da Luz!!!
ConclusõesO primeiro objetivo que devemos desejar alcançar quando fazemos uma mudularização é desenvolver um módulo com uma funcionalidade única irredutível, atômica. Quando você consegue isso está mais perto da luz, ponto pra vc.
O segundo objetivo é tornar esse módulo, que possui uma, apenas uma, funcionalidade única irredutível, o mais coeso possível e menos acoplado possível. Ou seja, conseguir fazer dele uma caixa preta. Quando você consegue isso está mais perto da luz, ponto pra vc.
O terceiro objetivo é conseguir o reaproveitamento da sub-rotina. Esse objetivo é ocupa um plano secundário em relação aos dois primeiros. O reaproveitamento de um módulo só traz benefícios efetivamente quando ele conseguiu antes atingir os dois anteriormente descritos. Do contrário ele será prejudicial, visto que o acoplamento gerado pelo reaproveitamento tornará seu sistema sensível a mudanças. Conseqüentemente, o processo de manutenção tanto evolutiva, quanto corretiva, será extremamente custoso. Em muitos casos tornando-se até mesmo inviável. Portanto, a argumentação, que defende a idéia de que a modularização não deve ser feita quando o reaproveitamento não será necessário, não se sustenta.
Concluindo, numa análise final, esse artigo também serviu para uma demonstração e entendimento da relação existente entre uma implementação OO e uma implementação estruturada. Aliais, a relação entre esses dois paradigmas de programação tem ganhado uma atenção especial aqui no estação ZN. Você pode ter certeza que isso não se deve ao acaso. Neste artigo podemos ver que não existe uma dualidade antagonistica entre esses paradigmas. Na minha opinião, não existe OO sem estruturação. Ou seja, um programador ou analista só fará bem OO se ele tiver muito bem consolidados os conceitos da estruturação. A conveniência de usar um ou outro vai depender de algumas variáveis, como por exemplo: A tecnologia que você estiver usando, a metodologia de engenharia adotada no projeto, ou a formação e cultura da equipe. Por exemplo, se você pretende conjugar estruturação e UML acho que encontrará alguma dificuldade para harmonizar o processo de analise com o de desenvolvimento. Presumo ... hehehhe!
Artigo completo (View Full Post)


